Refer to the image attached.
Given:
 and
and
 are congruent.
are congruent.
To Prove:
 is an isosceles triangle.
is an isosceles triangle.
Construction: Construct a perpendicular bisector from point B to line segment AC. Label the point of intersection between this perpendicular bisector and line segment AC as point D.
Proof:
Consider
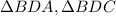

(By the definition of perpendicular bisector)
 (By the definition of perpendicular bisector)
(By the definition of perpendicular bisector)
So, Line segment AD is congruent to DC by the definition of perpendicular bisector.
 =
=
 (given)
(given)
So,
 by ASA congruence postulate.
by ASA congruence postulate.
∆BAD is congruent to ∆BCD by the ASA congruence Postulate.
Line segment AB is congruent to line segment BC because corresponding parts of congruent triangles are congruent (CPCTC).
So, Option C is the correct answer.