Question

with the polynomial provided I need help finding the zeros and putting them onto the graph as well as drawing the line correctly

Answer 1

Let's multiply out the polynomial first:

`\begin{gathered} f(x)=(x-1)(x+3)^2 \\ f(x)=(x-1)(x^2+6x+9) \\ f(x)=x^3+6x^2+9x-x^2-6x-9 \\ f(x)=x^3+5x^2+3x-9 \end{gathered}`

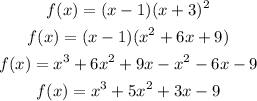
As we can see clearly that this is a cubic function, the highest degree is "3", which is odd. Hence,

This is an odd function.

Leading Coefficient is the number in front of the highest degree variable, that is x^3. So, there is "1" in front, thus the leading coefficient is positive.

Since we have one factor that is (x-1), it cuts the x-axis at:

x - 1 = 0

x = 1

We have another factor (x+3)^2. Since this is squared, here, the curve will bounce and touch the x-axis at:

(x+3)^2 = 0

x + 3 = 0

x = -3

Thus, the zeros are at x = 1 (cuts) and at x = -3 (bounces).

From basic cubic function (leading coefficient 0) we know as that x goes to infinity, the funtion goes to infinity. As x goes towards negative infinity, the function also approaches negative infinity.

Now, we can draw the curve: