Question

Kathleen and Arnob both run from the park entrance along a loop. Kathleen starts walking from the park entrance and gets a 5-mile head start on Arnob. The graph shows how far they have both traveled.

How many minutes does it take Arnob to catch up to Kathleen?

a. 9.8
b. 10
c. 73.5
d. 75

Answer 1

To solve the given problem above,

speed = distance over time

So look at the red line:
A travels 8 miles in 60 minutes, so his speed is 8 miles per hour while
K travels 2 miles in 30 minutes, so her speed is 4 miles per hour; K has a 5 mile head-start.

A's distance = initial distance from gate + (speed x time)
A's distance = 0 + (8 x time)

K's distance = initial distance from gate + (speed x time)
K's distance = 5 + (4 x time)

when they're the same distance from the gate, they've caught up with one another so when:

A's distance = K's distance
0 + (8 x time) = 5 + (4 x time)
8t = 5 + 4t
8t - 4t = 5
4t = 5
t = 5/4 hours
t = 1 hr and 15 mins
t = 75 mins

The answer is option D. I hope this helps.

Answer 2

For this case, the first thing we must do is define variables.

We have then:

x: time in minutes

y: distance traveled.

We then have the following equations:

For Kathleen:

`image`

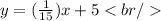
For Arnob:

`image`

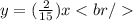
By the time Arnob reaches Kathleen we have:

`image`

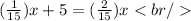
From here, we clear the value of x.

We have then:

`image`

`image`

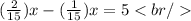
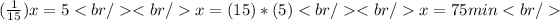
Answer:

it takes Arnob to catch up to Kathleen 75 minutes:

d. 75