Question

A commuter must pass through five traffic lights on her way to work, and will have to stop at each one that is red. She estimates the probability model for the number of red lights she hits, as shown below.

X= # of red P(x)
0 0.05
1 0.25
2 0.35
3 0.15
4 0.15
5 0.05
a. How many red lights should she expect to hit each day?
b. What's the standard deviation?
c. Find the mean and standard deviation of the number of red lights the commuter should expect to hit on her way during a 5 day work week.

Answer 1

a) 2 red lights

b) SD = 1.26

c) mean = 10, SD = 1.26

Explanation:

a) The number of red lights she expects to hit by day can be gotten by calculating the mean of the distribution.

`E(X) = \sum xP(x)`

`E(X) = (0*0.05) + (1*0.25) + (2*0.35) + (3*0.15) + (4*0.15) + (5*0.15)\\E(X) = 2.25`

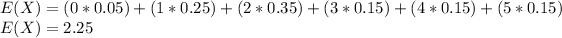
Since the number of lights cannot be a decimal, she expects to hit 2 lights each day

b)

Variance,
`V(X) = \sum(x- \mu)^(2) P(x)`

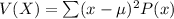
`V(X) = [(0-2.25)^(2)*0.05] + [(1-2.25)^(2)*0.25] + [(2-2.25)^(2)*0.35] + [(3-2.25)^(2)*0.15] + [(4-2.25)^(2)*0.15] + [(5-2.25)^(2)*0.05]`

V(X) = 0.253 + 0.391 + 0.022 + 0.084 + 0.459 + 0.378

V(X) = 1.587

Standard Deviation,
`SD = √(V(X))`

`SD = √(1.587)`

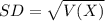
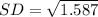
SD = 1.26

c) In a 5 day work week, the commuter is expected to hit an average of 5* 2 red lights, i.e. mean = number of red lights hit per day * number of days

mean = 2 * 5

mean = 10

The standard deviation will not change, SD = 1.26