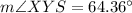Question

Transversal CD←→ cuts parallel lines PQ←→ and RS←→ at points X and Y, respectively. Points P and R lie on one side of CD←→, while Q and S lie on the other side. If

m∠PXY = 64.36°, what is m∠XYS?

Answer 1

Answer:
`64.36^(\circ)`

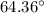
Explanation:

According to the question,

PQ ║ RS

And, PQ and RS are cut by the same transversal CD.

Then, By the alternative interior angle theorem,

The alternative interior angles made by the transversal CD on parallel lines PQ and RS must be congruent.

Thus,
`\angle PXY\cong \angle XYS`

⇒
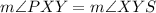`m\angle PXY = m\angle XYS` ( by the property of congruent angles )

Here
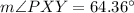
`m\angle PXY = 64.36^(\circ)`

⇒
`m\angle XYS = 64.36^(\circ)`

Answer 2

When parallel lines are cut by a transversal, then alternate interior angles are congruent.
Angles PXY and XYS are alternate interior angles.
m∠XYS = m∠PXY
Answer:
m∠XYS = 64.36°