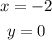Question

Find the solution for the system of linear equations-x + y = 2 and 2x + y = -4

Answer 1

`\begin{gathered} x=-2 \\ y=0 \end{gathered}`

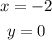
Explanation:

Given the system of equations:

`\begin{cases}-x+y=2 \\ 2x+y=-4\end{cases}`

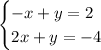
We'll multiply the first equation by 2:

`\begin{cases}-x+y=2 \\ 2x+y=-4\end{cases}\rightarrow\begin{cases}-2x+2y=4 \\ 2x+y=-4\end{cases}`

Then, we'll add up both equations and solve for y, as following:

`\begin{cases}-2x+2y=4 \\ 2x+y=-4\end{cases}\rightarrow3y=0\rightarrow y=0`

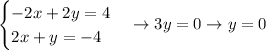
Now, we'll plug in this y-value in the second equation and solve for x, as following:

`\begin{gathered} 2x+y=-4 \\ \rightarrow2x+0=-4 \\ \rightarrow2x=-4 \\ \\ \Rightarrow x=-2 \end{gathered}`

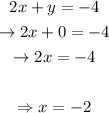
This way, we'll have that the solution to the system of linear equations is:

`\begin{gathered} x=-2 \\ y=0 \end{gathered}`