Answer:
Option C is correct
The value of the car is 0.94 times the value of the car the previous year.
Explanation:
Given the function:

where,
p(t) represents the value of a new car
t is the number of years.
We have to find the value 0.94 represent in this situation.
For t =0 years.
Initial value of car p(0) is 24,525
For t = 1 years
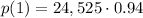
For t = 2 years
 and so on...
and so on...
Since;
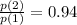
⇒
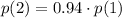
In general:
 where, t is the number of years.
where, t is the number of years.
⇒the value of the car is 0.94 times the value of the car the previous year.