Answer:
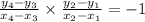
Explanation:
We know that,
If two line segments are perpendicular then the product of their slope is equal to -1,
Also, the slope of a line segment having the end points
 and
and
 is,
is,
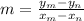
So, the slope of line segment AB having end points
 and
and
 is,
is,
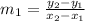
Similarly, the slope of line segment CD having end points
 and
and
 is,
is,
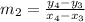
Hence, by the above property of perpendicular line segments ,
If AB and CD are perpendicular then,
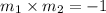
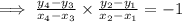
Third option is correct.