Question

A company sells product for $69 each. The variable costs are $9 per unit and fixed costs are $45,000 per month.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Define the revenue function TR

Total revenue is given as:

`Number\text{ of units sold }\cdot Cost\text{ per unit}`

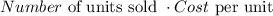
By calculation,

Let n represents the number of items sold

`\begin{gathered} By\text{ substitution,} \\ one\text{ item = \$69} \\ TR=69n \end{gathered}`

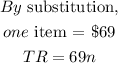
Total revenue cost is given as 69n

STEP 2: Define the Total cost function

The formula for total cost is given as:

`\begin{gathered} TC=an+b \\ where\text{ a is the unit cost} \\ n\text{ is the number of items } \\ b\text{ is the fixed cost} \end{gathered}`

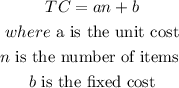
The known details from the given question are:

`\begin{gathered} a=\text{ \$}9 \\ n=n \\ b=\text{ \$}45000 \\ \\ TC=9n+45000 \end{gathered}`

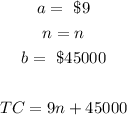
Total cost is given as 9n+45000

STEP 3: Calculate the number of units needed to be sold to break even

Here, we equate TC to TR and this is given as:

`\begin{gathered} TR=TC \\ 69n=9n+45000 \\ 69n-9n=45000 \\ 60n=45000 \\ n=(45000)/(60)=750 \end{gathered}`

Hence, 750 units are needed to be sold

STEP 4: Calculate the revenue at the break-even

We get this by substituting 750 for n in the Revenue function

`\begin{gathered} TR=69n \\ n=750 \\ TR=69(750)=\text{ \$}51750 \end{gathered}`

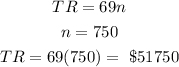
Hence, the TR at the breakeven is $51750