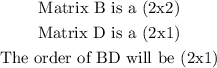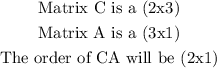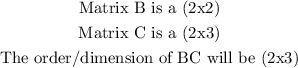Before two(2) matrices, say A and B can be multiplied together,to form AB, the number of the columns in A must be equal to the number of the rows in B.
The order/dimension of the resulting matrix, AB, will the combination of the number of rows in A and the number of columns in B.
For instance, if a matrix A has a dimension of ( p x q ) and a matrix B has a dimension of ( q x r ) to form matrix AB.
We can see that the number of columns in A, which is q, is equal to the number of rows in B, which is q also. Thus, the matrix are conformable i.e can be multiplied.
The order of the resulting matrix AB will have an order ( p x r ), as explained in the second statement above.
Hence, for the given problem, we have: