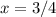Question

The perimeter of a square is equal to the perimeter of an equilateral triangle. The length of a side of the square is given by x, and the length of a side of the equilateral triangle is given by x=1. Which equation can be used to find the value of x?

Answer 1

To solve for x, given that the perimeter of a square is equal to the perimeter of an equilateral triangle, the equation 4x = 3(x + 1) can be used.

Step-by-step explanation:

To find the value of x when the perimeter of a square is equal to the perimeter of an equilateral triangle, we set up an equation. Since the side of the square is given by x, and the perimeter of a square is 4 times the length of a side, the perimeter of the square is 4x. The length of a side of the equilateral triangle is given by x + 1, and since the perimeter of the equilateral triangle is 3 times the length of a side, its perimeter is 3(x + 1). Setting these two perimeters equal to each other gives us the equation 4x = 3(x + 1).

Answer 2

The length of a side of the square is given by x

The length of a side of the equilateral triangle is given by x=1

Given is : The perimeter of a square is equal to the perimeter of an equilateral triangle.

Perimeter of square is given as 4 x side.

Perimeter of equilateral triangle is given as 3 x side.

So, we will make both equal.

`4x=3x`

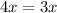
As x = 1 for triangle, the equation becomes:

`4x=3`

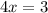
So,
`x=3/4`