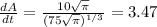Question

A machine starts dumping sand at the rate of 20 m3/min, forming a pile in the shape of a cone. The height of the pile is always twice the length of the base diameter.After 5 minutes, how fast is the area of the base increasing?

Answer 1

Start with Volume equation for a Cone in terms of base Area.

`V = (1)/(3) A h`
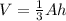
Next relate height in terms of base Area: (Note base = pi*r^2)

`h = 2D = 4r = 4 \sqrt {(A)/(\pi)}`
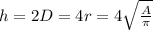
New volume equation is:

`V = (4)/(3 √(\pi)) A^(3/2)`
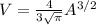
Take derivative with respect to time:

`(dV)/(dt) = ((4)/(3√(\pi)))((3)/(2)) √(A) (dA)/(dt)`
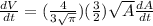
Sub in rate for volume, solve for dA/dt

`(dA)/(dt) = (10 √(\pi))/(√(A))`
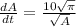
Finally we need the Area after 5 min, given the volume after 5 min is 100.
Go back to Volume equation and solve for sqrt(A)

`100 = (4)/(3 √(\pi)) (√(A))^3 \\ √(A) = (75 √(\pi))^(1/3)`
Final Answer:

`(dA)/(dt) = (10 √(\pi))/((75 √(\pi))^(1/3)) = 3.47`