Question

If a line connected point S to point Q, what would be the slope of the line?

A) 3
B) 3/2
C) 2/3
D) -2/3
the first graph
What is the solution to the system of equations shown in the graph?
A) (0, 5)
B) (-2, 1)
C) (0, -1)
D) (1, -2)
the second graph

Answer 1

It rises 15 and goes over 10. Slope is rise/run. So 15/10 or 3/2.
The solution to #2 is where they intersect. (-2,1)

Answer 2

Ques 1)

B) 3/2

Ques 2)

B) (-2,1)

Explanation:

Ques 1)

We know that the coordinates of points S are (-2,-8)

and the coordinates of the point Q are: (8,7)

We know that the slope of a line passing segment with end points (a,b) and (c,d) are given as:

`slope=(d-b)/(c-a)`

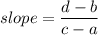
Here we have:

(a,b)=(-2,-8) and (b,d)=(8,7)

Hence, the slope is:

`Slope=(7-(-8))/(8-(-2))\\\\Slope=(7+8)/(8+2)\\\\Slope=(15)/(10)\\\\Slope=(3)/(2)\\(Since\ both\ the\ numerator\ and\ denominator\ are\ divisible\ by\ 5)`

Hence, the slope of a line connecting point S to point Q is:

3/2.

Ques 2)

We know that solution of a system of equation is the point where the two system meet if it has a unique solution.

From the graph of the system of equation we could observe that the two lines intersect each other in the second quadrant and we know that the point in the second quadrant has x-value negative and y-value positive.

Hence, the point that is the solution of the given system of equations is:

B) (-2,1)