Question

I need help number 7

Answer 1

Linear and Exponential Functions

Both linear and exponential functions are widely used to model facts of life. Conversely, the exponential function is best suited for cases where the change of the values depends on the actual values.

The linear function usually grows or decays at a fixed rate.

a.

Air freshener A has an initial mass of 47 grams and it decreases by 3.4 grams each day. Being t the number of days, the equation for the mass of the air freshener A is:

`m_A=47-3.4t`

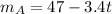
b.

Air freshener B has an initial mass of 47 grams and it decreases by 3.4% each day.

The equation for the mass of the air freshener B is:

`\begin{gathered} m_B=47\cdot(1-0.034)^t \\ m_B=47\cdot0.966^t \end{gathered}`

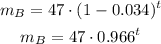
c. Analyze each statement and establish if it's true or false.

* Air freshener B will eventually have a mass of 0 grams. As mentioned above, the exponential model has a decrease or increase rate that depends on the current value (or mass). Since we will always have some mass, the next value will be less than the previous one, but never zero. It can be checked when looking at the exponential function graph. It never reaches 0. This statement is false (unchecked).

* It takes longer to air freshener A to reach a mass of 25 grams than air freshener B. Let's check it. From the model of A:

`\begin{gathered} m_A=47-3.4t=25 \\ \text{Solving for t:} \\ t=(25-47)/(-3.4)=6.47days \end{gathered}`

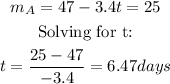
Substituting this value of t in B:

`m_B=47\cdot0.966^(6.47)=37.58grams`

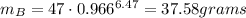
So, when A has 25 grams, B has 37.58 grams. This statement is false because B needs more time to reach 25 grams.

* 5 days after being opened, air freshener A will have a larger mass than air freshener B. Let's substitute t=5 in both models:

`\begin{gathered} m_A=47-3.4*5 \\ m_A=47-17=30grams \end{gathered}`
`m_B=47\cdot0.966^5=39.54\text{ grams}`

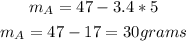
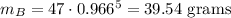
This statement is false. Unchecked.

* Air freshener A will eventually have a mass of 0 grams.

This is true because we can solve the equation for t:

`\begin{gathered} t=(47-m_A)/(3.4) \\ t=(47-0)/(3.4)=13.82days \end{gathered}`

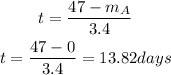
This sentence is true. Checked