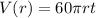Question

A cone with a fixed height of 15 inches is shown on a computer screen. An animator increases the radius r at a rate of 6 inches per minute. Which of the following gives the volume v(r) of the cone as a function of time f(t)? Assume the radius is 6 inches at t = 1.

Answer 1

Answer::

`V(r)=60\pi rt`

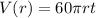
Step-by-step explanation:

For a cone of radius r and height, h

`\text{Volume}=(1)/(3)\pi r^2h`

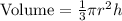
The cone has a fixed height of 15 inches.

The radius increases at a rate of 6 inches per minute.

We have that:

`\begin{gathered} V=(1)/(3)\pi*15r^2 \\ V=5\pi r^2 \end{gathered}`

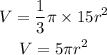
Taking the derivative with respect to time(t), we have:

`\begin{gathered} (dV)/(dt)=5\pi2r(dr)/(dt) \\ Since\text{ }\frac{dr}{\mathrm{d}t}=6\text{ inches per minute} \\ (dV)/(dt)=5\pi2r*6 \\ (dV)/(dt)=60\pi r \end{gathered}`

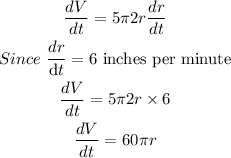
We then rewrite in order to integrate.

`\begin{gathered} dV=60\pi\text{rdt} \\ \int dV=\int 60\pi\text{rdt}=60\pi\int \text{rdt} \\ V=60\pi rt+C,C\text{ a constant of integration} \end{gathered}`

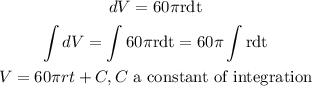
Therefore, we have:

`V(r)=60\pi rt`