Question

The radius of a sphere is tripled. What happens to the volume?Hint: Test two scenarios and compare the volumes! Show your work. Used 3.14 for piC. It is 15 times largerD. It is 27 times largerA. It triplesB. It quadruples

Answer 1

First, we need to test two scenarios using the sphere volume formula:

The volume for a sphere is given by:

`A_s=(4)/(3)\pi r^3`

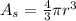
Let us set r=3

Then:

`\begin{gathered} A_(s)=(4)/(3)\pi r^(3) \\ A_s=(4)/(3)\pi(3)^3 \\ A_s=36\pi \\ A_s=113.04 \end{gathered}`

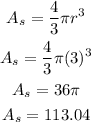
If we tripled the radio= 3r = 3(3)= 9. Then:

`\begin{gathered} A_s=(4)/(3)\pi(9)^3 \\ A_s=3052.08 \end{gathered}`

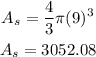
Now, we need to compare both results:

A1 = 113.14

A2 = 3052.08

If we multiply A1 by 27=

27(113.14) = 3052.08

Hence, the volume when the radius is tripled is the product of the first volume by 27.

Therefore, the correct answer is option D.It is 27 times larger