To solve this problem, let's use binominal distribution.
To calculate the probability of an event (P), use the formula below.
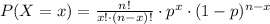
Where
n = number total of events;
x = number of favorable events;
p = probability of a single event.
In this exercise:
n = 9
x = 5
p = 0.61
Then, substituting the values:
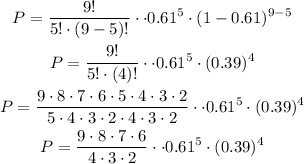
Solving the expression:
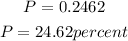
Answer: P = 0.2462.