Question

Assume that when adults with smartphones are randomly selected, 61% use them in meetings or classes. If 9 adult smartphone users are randomly selectedfind the probability that exactly 5 of them use their smartphones in meetings or classes.

Answer 1

To solve this problem, let's use binominal distribution.

To calculate the probability of an event (P), use the formula below.

`P(X=x)=(n!)/(x!\cdot(n-x)!)\cdot p^x\cdot(1-p)^(n-x)`

Where

n = number total of events;

x = number of favorable events;

p = probability of a single event.

In this exercise:

n = 9

x = 5

p = 0.61

Then, substituting the values:

`\begin{gathered} P=(9!)/(5!\cdot(9-5)!)\cdot\cdot0.61^5\cdot(1-0.61)^(9-5) \\ P=(9!)/(5!\cdot(4)!)\cdot\cdot0.61^5\cdot(0.39)^4 \\ P=(9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2)/(5\cdot4\cdot3\cdot2\cdot4\cdot3\cdot2)\cdot\cdot0.61^5\cdot(0.39)^4 \\ P=(9\cdot8\cdot7\cdot6)/(4\cdot3\cdot2)\cdot\cdot0.61^5\cdot(0.39)^4 \\ \end{gathered}`

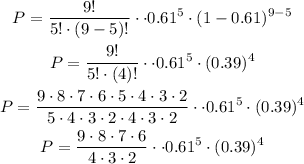
Solving the expression:

`\begin{gathered} P=0.2462 \\ P=24.62percent_{} \end{gathered}`

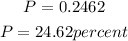
Answer: P = 0.2462.