First let's draw the vectors that correspond to the boat speed and the river speed.
The river speed is 2 m/s due east, and the boat speed is 3 m/s due north, so we have:
Addind these vectors, the resultant is:
In order to calculate the angle x, we can use the tangent relation, which is the opposite side to the angle over the adjacent side to the angle:
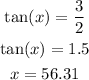
So the direction of the resultant is 56 degrees.