Question

Alice drew a rectangle with a perimeter of 30 cm and an area of 56 cm2. Which dimensions match Alice's rectangle?

Answer 1

The dimensions that match Alice's rectangle are 7 cm and 8 cm.

Explanation:

The perimeter of the rectangle is given by:

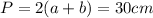`P = 2(a + b) = 30 cm` (1)

Where a and b are the sides of the rectangle

Also, the area of the rectangle is:

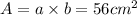`A = a* b = 56 cm^(2)` (2)

By solving equation (1) for a, we have:

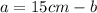`a = 15 cm - b` (3)

Now, by entering equation (3) into (2) we can find one side of the rectangle:

`56 cm^(2) = (15 cm - b)* b`

`b^(2) - 15b + 56 = 0`

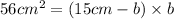
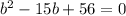
Solving the above quadratic equation we have:

b₁ = 7 cm and b₂ = 8 cm

Now, the other side of the rectangle can be calculated with equation (3):

`a = 15 cm - b_(1) = 15 - 7 cm = 8 cm`

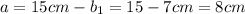
or

`a = 15 cm - b_(2) = 15 - 8 cm = 7 cm`

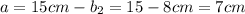
Taking the first solution (b₁) or the second (b₂), we find that the dimensions that match Alice's rectangle are 7 cm and 8 cm.

Therefore, the dimensions that match Alice's rectangle are 7 cm and 8 cm.

I hope it helps you!