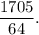Question

What is the sum of the first five terms of a geometric series with a1 = 20 and r = 1/4?

Answer 1

The first term is 20 The second term is 20* 1/4 = 5 The third term is 5 * 1/4 = 5/4 The 4th term is 5/4 * 1/4 = 5/16 The 5th term is 5/16 * 1/4 = 5/64 Sum is therefore 20 + 5 + 5/4 + 5/16 + 5/64 = (1280 + 320 + 80 + 20 + 5) / 64 = 1705/64

Answer 2

Answer: The required sum of first terms of the series is
`(1705)/(64).`

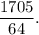
Step-by-step explanation: We are given to find the sum of the first five terms of a geometric series with first term and common ratio as follows :

`a_1=20~~~~~\textup{and}~~~~~r=(1)/(4).`

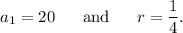
We know that

the sum of first n terms of a geometric series with first term
`a_1` and common ratio r is given by

`S_n=(a(1-r^n))/(1-r).`

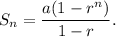
Therefore, the sum of first 5 terms of the given geometric series is given by

`S_5\\\\\\=(a(1-r^5))/(1-r)\\\\\\=(20(1-((1)/(4))^5))/(1-(1)/(4))\\\\\\=(20\left(1-(1)/(1024)\right))/((3)/(4))\\\\\\=20*(4)/(3)*(1023)/(1024)\\\\\\=20*(341)/(256)\\\\\\=(5* 341)/(64)\\\\\\=(1705)/(64).`

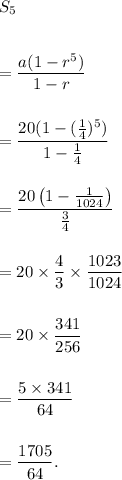
Thus, the required sum of first terms of the given geometric series is
`(1705)/(64).`