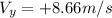Question

A soccer player kicks a soccer ball at +10.0 m/s at an angle of 60°. What are the horizontal and vertical components of velocity of the kick?

Answer 1

This seems like a calculus problem. I'm assuming you would use cos and sin. so here's the vertical component +10.0m/s multiplied by sin60 = 8.66 rounded to the hundreths place. Now for horizontal, that would be +10.0m/s multiplied by cos60 = 5. hope this helped.

Answer 2

Horizontal component:
`V_(x)=+5m/s`

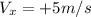
Vertical component:
`V_(y)=+8.66m/s`

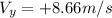
Step-by-step explanation:

We have the launch speed
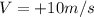`V =+ 10m/s` and the angle of 60°, so the components of the speed
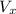`V_(x)` and
`V_(y)` are those shown in the attached image.

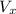`V_(x)` which is the horizontal component of the velocity can be found by multiplying the cosine of the angle by the initial velocity:

`V_(x)=+10m/s(cos60)\\V_(x)=+10m/s(0.5)\\V_(x)=+5m/s`

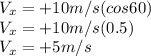
`V_(y)` which is the verticalcomponent of the velocity is found by multiplying the sine of angle by the initial velocity

`V_(y)=+10m/s(sin60)\\V_(y)=+10m/s(0.866)\\V_(y)=+8.66m/s`

In summary:

Horizontal component:
`V_(x)=+5m/s`

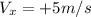
Vertical component:
`V_(y)=+8.66m/s`