Question

If ABC ~ DEC, solve for x. The image is not drawn to scale.

A.
x = 2
B.
x = 3
C.
x = 4
D.
x = 13

Answer 1

`If\ \Delta ABC\sim\Delta DEC\ then:\\\\(19-2x)/(11-x)=(8+x)/(6)\ where\ x\in(-8;\ 11)\ \ \ |cross\ multiply\\\\(11-x)(8+x)=6(19-2x)\\11(8)+11(x)-x(8)-x(x)=6(19)+6(-2x)\\88+11x-8x-x^2=114-12x\\-x^2+3x+88=114-12x\ \ \ |subtract\ 114\ from\ both\ sides\\-x^2+3x-26=-12x\ \ \ \ \ |add\ 12x\ to\ both\ sides\\-x^2+15x-26=0\ \ \ \ |change\ signs\\x^2-15x+26=0\\x^2-2x-13x+26=0\\x(x-2)-13(x-2)=0\\(x-2)(x-13)=0\iff x-2=0\ or\ x-13=0\\\\x=2\in(-8;\ 11)\ or\ x=13\\otin(-8;\ 11)\\\\Answer:\boxed{\boxed{A.\ x=2}}`

Answer 2

Answer: A. x = 2

Explanation:

In the given picture we have
`\triangle{ABC}\sim\triangle{DEC}`

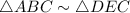
Since, we know that the corresponding sides in similar triangles are in proportion.

Therefore, we have

`(CD)/(AC)=(CE)/(BC)\\\\\Rightarrow(8+x)/(6)=(19-2x)/(11-x)\\\\\Rightarrow\ (11-x)(8+x)=6(19-2x)\\\\\Rightarrow\ 88 + 3x -x^2=114-12x\\\\\Rightarrow x^2-15x+26=0\\\\\Rightarrow\ (x-13)(x-2)=0\\\\\Rightarrow\ x=13,2`

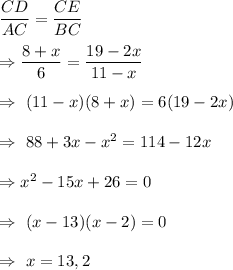
But x can not be 13 because BC=11-13=-2, which is not possible.

Therefore, the value of x=2.