Question

What is a possible value for the missing term of the geometric sequence?

50, ___, 450,

Answer 1

Explanation:

One five zero

Answer 2

Geometric sequence states that a sequence in which a number that follows the pattern were the next term is found by multiplying the constant common ratio term(r).

For the sequence:
`a, ar, ar^2, ar^3,.....`

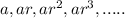
The formula for the nth geometric sequence is given by:

`a_n =ar^(n-1)`

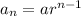
where

a is the first term

r is the common ratio

n is the number of terms.

Given that:

A geometric sequence:

50, _
`a_2`___, 450

Here, a = first term = 50

`a_3 = 450`

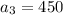
Using the nth geometric sequence formula:

`a_3 = ar^2`

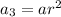
or

`ar^2 = 450`

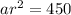
Substitute the value of a , to solve for r;

`50r^2 = 450`

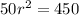
Divide both sides by 50 we get;

`r^2 = 9`

`r = √(9) = 3`

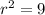
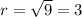
To find the term
`a_2`;

`a_2 = ar`

Substitute the given values we have;

`a_2 = 50 \cdot 3 = 150`

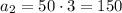
Therefore, the possible value for the missing term of the geometric sequence is 150