Answer:
The simplified form of the given expression

Explanation:
Given expression

We have to simplify the given expression

Consider the given expression

Consider denominator
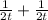
Apply rule,
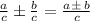
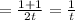
Now, apply fraction rule,

We get,
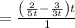
Simplify, we get,
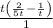
Simplify, we get,
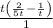
Further simplify by
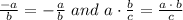
We get,

Thus,
