Question

Which of the following is the expansion of (3c + d2)6?

A) 729c6 + 1,458c5d2 + 1,215c4d4 + 540c3d6 + 135c2d8 + 18cd10 + d12

B) 729c6 + 1,458c5d + 1,215c4d2 + 540c3d3 + 135c2d4 + 18cd5 + d6

C) 729c6 + 1,215c5d2 + 810c4d4 + 270c3d6 + 90c2d8 + 15cd10 + d12

D) 729c6 + 243c5d2 + 81c4d4 + 27c3d6 + 9c2d8 + 3cd10 + d12

E) c6 + 6c5d2 + 15c4d4 + 20c3d6 + 15c2d8 + 6cd10 + d12

Answer 1

Option (a) is correct.

`(3c+d^2)^6=729c^6+1458c^5d^2+1215c^4d^4+540c^3d^6+135c^2d^8+18cd^(10)+d^(12)`

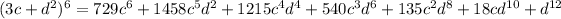
Step-by-step explanation:

Given :
`\left(3c+d^2\right)^6`

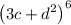
We have to expand the given expression and choose the correct from the given options.

Consider the given expression
`\left(3c+d^2\right)^6`

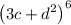
Using binomial theorem ,

`\left(a+b\right)^n=\sum _(i=0)^n\binom{n}{i}a^(\left(n-i\right))b^i`

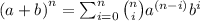
We have
`a=3c,\:\:b=d^2`

`=\sum _(i=0)^6\binom{6}{i}\left(3c\right)^(\left(6-i\right))\left(d^2\right)^i`

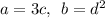
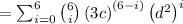
also,
`\binom{n}{i}=(n!)/(i!\left(n-i\right)!)`

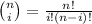
for i = 0 , we have,

`(6!)/(0!\left(6-0\right)!)\left(3c\right)^6d^2^0=729c^6`

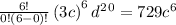
for i = 1 , we have,

`(6!)/(1!\left(6-1\right)!)\left(3c\right)^5d^2^1=1458c^5d^2`

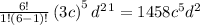
for i = 2 , we have,

`(6!)/(2!\left(6-2\right)!)\left(3c\right)^4d^2^2=1215c^4d^4`

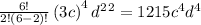
for i = 3 , we have,

`(6!)/(3!\left(6-3\right)!)\left(3c\right)^3d^2^3=540c^3d^6`

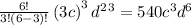
for i = 4 , we have,

`(6!)/(4!\left(6-4\right)!)\left(3c\right)^2d^2^4=135c^2d^8`

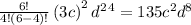
for i = 5 , we have,

`(6!)/(4!\left(6-4\right)!)\left(3c\right)^2d^2^4=18cd^(10)`

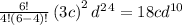
for i = 6 , we have,

`(6!)/(6!\left(6-6\right)!)\left(3c\right)^0d^2^6=d^(12)`

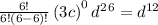
Thus, adding all term together, we have,

`(3c+d^2)^6=729c^6+1458c^5d^2+1215c^4d^4+540c^3d^6+135c^2d^8+18cd^(10)+d^(12)`

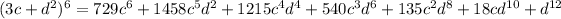
Thus, Option (a) is correct.

Answer 2

Answer: Option A)
`729c^6 + 1,458c^5d^2 + 1,215c^4d^4 + 540c^3d^6 + 135c^2d^8 + 18cd^(10) + d^(12)` is the correct expansion.

Step-by-step explanation:

on applying binomial theorem,
`(a+b)^n=\sum_(r=0)^(n) (n!)/(r!(n-r)!) a^(n-r) b^r`

Here a=3c,
`b=d^2` and n=6,

Thus,
`(3c+d^2)^6=\sum_(r=0)^(6) (6!)/(r!(6-r)!) (3c)^(n-r) (d^2)^r`

⇒
`(3c+d^2)^6= (6!)/((6-0)!0!) (3c)^(6-0).(d^2)^0+(6!)/((6-1)!1!) (3c)^(6-1).(d^2)^1+(6!)/((6-2)!2!) (3c)^(6-2).(d^2)^2+(6!)/((6-3)!3!) (3c)^(6-3).(d^2)^3+(6!)/((6-4)!4!) (3c)^(6-4).(d^2)^4+(6!)/((6-5)!5!) (3c)^(6-5).(d^2)^5+(6!)/((6-6)!6!) (3c)^(6-6).(d^2)^6`

⇒
`(3c+d^2)^6= (6!)/((6-)!0!) (3c)^6.d^0+(6!)/((5)!1!) (3c)^5.d^2+(6!)/((4)!2!) (3c)^4.d^4+(6!)/((6-3)!3!) (3c)^3.d^6+(6!)/((2)!4!) (3c)^2.d^8+(6!)/((1)!5!) (3c).d^(10)+(6!)/((0)!6!) (3c)^0.d^(12)`

⇒
`(3c+d^2)^6=(3c)^6.d^0+(720)/(120) (3c)^5.d^2+(720)/(48) (3c)^4.d^4+(720)/(36) (3c)^3.d^6+(720)/(48) (3c)^2.d^8+(720)/(120) (3c).d^(10)+.d^(12)`

⇒
`(3c+d^2)^6=729c^6 + 1,458c^5d^2 + 1,215c^4d^4 + 540c^3d^6 + 135c^2d^8 + 18cd^(10) + d^(12)`