Newton's gravitational force states that the force a gravity between two objects is given by:
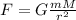
The gravitational acceleration is defined as the acceleration exerted by a mass in another and it is related to the weight of the mass as:
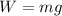
Plugging this force in Newton's gravitational law we have that:
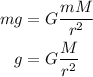
Let's assume M and r are the mass and raidus of earth respectively, then we have that the gravitational acceleration on earth is:
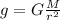
Now, in planet Nelson the mass is 4 times that of earth and its raidus if four times the raidus on earth, then we have:
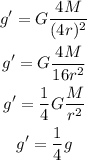
Therefore, the acceleration of gravity in planet Nelson is 1/4 the acceleration of gravity on earth.