Question

In another solar system is a planet Nelson, which has 4 times the mass of the Earth and also 4 times the radius? How does the gravitational acceleartion on thesurface of Nelson compare to the gravitational acceleration on the surface of the Earth?

Answer 1

Newton's gravitational force states that the force a gravity between two objects is given by:

`F=G(mM)/(r^2)`

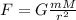
The gravitational acceleration is defined as the acceleration exerted by a mass in another and it is related to the weight of the mass as:

`W=mg`

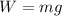
Plugging this force in Newton's gravitational law we have that:

`\begin{gathered} mg=G(mM)/(r^2) \\ g=G(M)/(r^2) \end{gathered}`

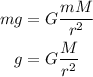
Let's assume M and r are the mass and raidus of earth respectively, then we have that the gravitational acceleration on earth is:

`g=G(M)/(r^2)`

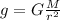
Now, in planet Nelson the mass is 4 times that of earth and its raidus if four times the raidus on earth, then we have:

`\begin{gathered} g^(\prime)=G(4M)/((4r)^2) \\ g^(\prime)=G(4M)/(16r^2) \\ g^(\prime)=(1)/(4)G(M)/(r^2) \\ g^(\prime)=(1)/(4)g \end{gathered}`

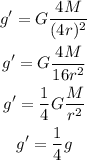
Therefore, the acceleration of gravity in planet Nelson is 1/4 the acceleration of gravity on earth.