To answer this question we will graph the solution set of each inequality and then find the intersection of the solution sets.
1)
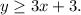
Since the inequality is not strict, then the border of the solution set is a solid line.
Notice that the solution set of the first inequality consists of all the points on the graph and above the graph of the line:
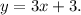
Therefore the solution set to the first inequality is:
2)
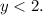
The solution set of the above inequality consists of all the points such that its y-coordinate is less than 2, then its graph is:
Therefore the solution set to the given system of inequalities is:
Answer:
Two points on the solution set are (-2,-3) and (-1,0) and two points that are not on the solution set are (-2,2) and (-4,2).