Question

**!!!STUCK ON 2 QUESTIONS!!!!

The time is takes to mow the lawn at a large park m(x) varies inversely with the numbers of workers assigned to the job x. It takes 90 minutes to complete the job when 3 workers are assigned to it.


which equation can be used to find the time to complete the job when x workers are assigned to it?

A.) m(x)= 270/x
B.) m(x) = 270x
C.) m(x) = 30/x
D.) m(x) = 30x

2. Suppose that H(x) varies inversely with x and H(x)=50 when x =0.25

What is H(x) when x =2?

A.) 0.5
B.) 6.25
C.) 12.5
D.) 24

Can you also provide how you got the answer as well :)

Answer 1

The first one is A
270/3=90 thus proving the equation right

oh and the second one is B

Answer 2

1. Which equation can be used to find the time to complete the job when x workers are assigned to it?

A.) m(x) = 270/x

2. Suppose that H(x) varies inversely with x and H(x)=50 when x =0.25

What is H(x) when x =2?

B.) 6.25

Explanation:

1. We know when x=3 (workers), m(x)= 90 min (time is takes to mow the lawn at a large park) and we know m(x) varies inversely with x, this means when m(x) increases so x decreases. This is obtained with a division over x.

Now, we can replace to know what is the correct answer:

`m(x)=(y)/(x) (1) \\90=(y)/(3) \\90*3=y`

`y=270`

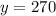
The answer is A.

`m(x)=(270)/(x)`

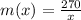
We can confirm if we replace x=3 in the equation before. Our answer should be 90.

`m(x)=(270)/(3)=90`

2. Suppose that H(x) varies inversely with x and H(x)=50 when x =0.25

We know H(x) varies inversely with x, this means when H(x) increases so x decreases. This is obtained with a division over x. Now, we need to find the constant in the numerator.

Now, we can replace in the eq (1) to know the constant in the numerator:

`H(x)=(y)/(x)\\50=(y)/(0.25) \\50*0.25=y`

`y=12.5`

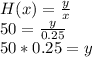
Now, we can replace in the eq (1) to find H(x) when x=2

`m(x)=(y)/(x)`

`m(x)=(12.5)/(2)`

`m(x)=6.25`

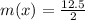
The answer is B.) 6.25