Question

(04.02 LC)

Triangle ABC is similar to triangle PQR, as shown below:

Two similar triangles ABC and PQR are shown. Triangle ABC has sides AB = c, BC = a, and AC = b. Triangle PQR has sides PQ = r,
Which ratio is equal to b:q? (1 point)


b:a

c:r

r:a

q:c

Answer 1

∆ABC~∆PQR

AB~PQ , c~r

c:r

Answer 2

The correct option is 2.

Explanation:

It is given that triangles ABC and PQR are similar triangles.

The sides of the triangle ABC are AB = c, BC = a, and AC = b. Triangle PQR has sides PQ = r, QR=p and PR=q.

If two triangles are similar, then their corresponding sides proportional.

Since ABC and PQR are similar triangles, therefore

`(AB)/(PQ)=(BC)/(QR)=(AC)/(PR)`

`(c)/(r)=(a)/(p)=(b)/(q)`

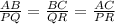
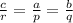
It can be written as

`(c)/(r)=(b)/(q)`

`(a)/(p)=(b)/(q)`

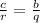
Therefore b:q is equal to c:r or a:p. Option 2 is correct.