Question

The axis of symmetry for the function f(x) = –2x2 + 4x + 1 is the line x = 1. Where is the vertex of the function located?

Answer 1

(1,3)

Explanation:

Answer 2

(1, 3)

Explanation:

You are given the h coordinate of the vertex as 1, but in order to find the k coordinate, you have to complete the square on the parabola. The first few steps are as follows. Set the parabola equal to 0 so you can solve for the vertex. Separate the x terms from the constant by moving the constant to the other side of the equals sign. The coefficient HAS to be a +1 (ours is a -2 so we have to factor it out). Let's start there. The first 2 steps result in this polynomial:

`-2x^2+4x=-1`. Now we factor out the -2:

`-2(x^2-2x)=-1`. Now we complete the square. This process is to take half the linear term, square it, and add it to both sides. Our linear term is 2x. Half of 2 is 1, and 1 squared is 1. We add 1 into the set of parenthesis. But we actually added into the parenthesis is +1(-2). The -2 out front is a multiplier and we cannot ignore it. Adding in to both sides looks like this:

`-2(x^2-2x+1)=-1-2`. Simplifying gives us this:

`-2(x^2-2x+1)=-3`

On the left we have created a perfect square binomial which reflects the h coordinate of the vertex. Stating this binomial and moving the -3 over by addition and setting the polynomial equal to y:

`-2(x-1)^2+3=y`

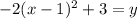
From this form,

`y=-a(x-h)^2+k`

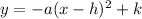
you can determine the coordinates of the vertex to be (1, 3)