Answer:
Distance traveled by bicyclist traveling west = 15 miles
Explanation:
Two bicyclists leave the center of town at the same time. One heads due north and the other heads due west. Later, the two cyclists are exactly 25 mi apart. The cyclist headed north has traveled 5 mi farther than the cyclist going west.
These two cyclists travel at angle 90°
Relative displacement can be calculated using Pythagoras theorem.
Let d be the distance traveled by bicyclist traveling west
Distance traveled by bicyclist traveling north = d + 5
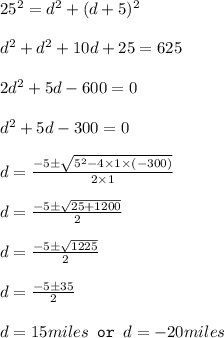
Negative displacement is not possible.
Hence d = 15 miles
Distance traveled by bicyclist traveling west = d = 15 miles