Question

Find the arc length of a central angle 300 degrees in a circle whose radius is 2 inches? help now ASP I NEED HELP A.10 π/ 3 in

B.1200 in
C. 22 π/ 3 in
D. 75 in.

Answer 1

`\text{Arc length } = (\theta)/(360)2\pi r`


`= ((300)/(360))2\pi (2)`


`= 4\pi((300)/(360))`


`= 4\pi((5)/(6))`


`= (20\pi)/(6)`


`= (10\pi)/(3) \text{ in}`

Answer 2

Answer: A.
`(10)/(3)\pi\ in.`

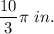
Explanation:

The formula to calculate the arc length with central angle x and radius r given by :-

`l=(x)/(360^(\circ))*2\pi r`

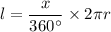
Given: Radius of circle 'r'= 2 inches

The central angle 'x'=
`300^{\circ]`

Now, the arc length of a central angle
`300^{\circ]` in a circle whose radius is 2 inches is given by :-