Question

Part 3: Use a series to solve a problem. Melissa has started training for a race. The first time she trains, she bikes 5 miles. Each subsequent time she trains, she bikes 0.5 mile farther than she did the previous time. a) Use summation notation to write an arithmetic series to represent the total distance Melissa has biked after she has trained n times. (2 points) b) Use the formula for a partial sum of the series you wrote in part a, above, to answer this question: What is the least number of times Melissa must bike for her total distance biked during training to exceed 60 miles? (3 points)

Answer 1

a)

First term= a1 = 5

common difference = d = 0.5

an= a1 + d (n-1)

an= 5 + 0.5 (n-1)

an= 5 + 0.5n - 0.5

an= 4.5 + 0.5n

`dn=\sum ^n_(k=1)(4.5+0.5k)`

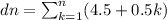
b) Sum of terms of an arithmetic series is the average of the first and last, multiplied by the number of terms: the sum must be greater than 60.

dn = n/2 (5 + 4.5 + 0.5n)

n/2 (9.5 + 0.5n) > 60

n (19+n) > 240

n^2 +19n + 9.5^2 > 240 +9.5^2

n+9.5 > √330.25

n> 18.17 -9.5

n> 8.67

Melissa's total distance will first exceed 60 miles the 9th time she trains.