1) We have a parallelogram with the following sides and properties:
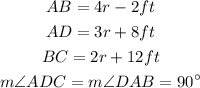
We want to know how many feets of fencing are needed to enclose the parallelogram, i.e. we must calculate the parallelogram's perimeter. The perimeter of the parallelogram is simply the sum of the lengths of the sides:
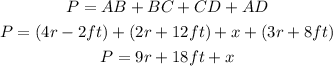
We see that there is a side, DC = x, for which we don't know its length, so we must find the value of x to calculate the perimeter P, let's do that.
From the picture above we have the right triangle △CEB, with the following sides:
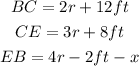
Where BC is the hypotenuse (h) of the triangle, CE (a) and EB (b) the cathetus of the triangle. We can apply Pythagoras Theorem to find x in the following way:
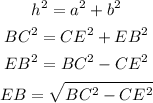
Now, we replace we values of BC and CE in the last equation and find that:
![\begin{gathered} EB=\sqrt[]{(2r+12ft)^2-(3r+8ft)^2} \\ EB=\sqrt[]{4r^2+144ft^2+48r\cdot ft-9r^2-64ft^2-48r\cdot ft} \\ EB=\sqrt[]{80ft^2-5r^2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/7xivp2gr9snkpgknea0b.png)
Now, using the value of EB in terms of x we can find the value of x:
![\begin{gathered} EB=4r-2ft-x=\sqrt[]{80ft^2-5r^2} \\ x=4r-2ft-\sqrt[]{80ft^2-5r^2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/4jo9adz8lftef5vznwyj.png)
Finally, replacing the value of x in the equation above for the perimeter we find:
![\begin{gathered} P=9r+18ft+x \\ P=9r+18ft+4r-2ft-\sqrt[]{80ft^2-5r^2} \\ P=13r+16ft-\sqrt[]{80ft^2-5r^2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/ydm8zg7by4anpwlq9miy.png)
2) If instead, we have the following data for the parallelogram: