Question



Which points are solutions to the linear inequality y < 0.5x + 2? Check all that apply.

(–3, –2)  

(–2, 1)

(–1, –2)

(–1, 2)

(1, –2)

(1, 2)

Answer 1

The answer is (1,-2) and (1,2)

Answer 2

Points (-3,-2), (-1,-2), (1,-2) and (1,2) are solutions to the given inequality.

Explanation:

We are given the following inequality in the question:

`y < 0.5x + 2`

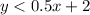
We have to check which points give the solution to the given inequality.

1) (-3,-2)

Putting the values in the given inequality:

`-2 < 0.5* (-3) + 2\\-2 < 0.5\\\text{which is true}`

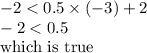
The above point is a solution to the given inequality.

2) (-2,1)

Putting the values in the given inequality:

`1 < 0.5* (-2) + 2\\1 < 1\\\text{which is not true}`

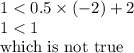
The above point is not a solution to the given inequality.

3) (-1,-2)

Putting the values in the given inequality:

`-2 < 0.5* (-1) + 2\\-2 < 1.5\\\text{which is true}`

The above point is a solution to the given inequality.

4) (-1,2)

Putting the values in the given inequality:

`2< 0.5* (-1) + 2\\2 < 1.5\\\text{which is not true}`

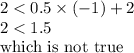
The above point is not a solution to the given inequality.

5) (1,-2)

Putting the values in the given inequality:

`-2 < 0.5* (1) + 2\\-2 < 2.5\\\text{which is true}`

The above point is a solution to the given inequality.

6) (1,2)

Putting the values in the given inequality:

`2 < 0.5* (1) + 2\\2 < 2.5\\\text{which is true}`

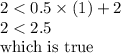
The above point is a solution to the given inequality.

Points (-3,-2), (-1,-2), (1,-2) and (1,2) are solutions to the given inequality.