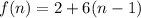Question

Find a polynomial function f(n) such that f(1), f(2), ... , f(8) is the following sequence.2, 8, 14, 20, 26, 32, 38, 44

Answer 1

We can recognize the sequence is an arithmetic progression by noticing that the common difference between each term is 6.

`f(n) = a+(n-1)d`
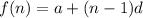
where f(n) is the sequence
n is the term number
d is the common difference
and a is the starting term

We are well aware that our starting term, and hence a, is 2 and our difference, and hence d, is 6.
So our polynomial function is

`f(n) = 2+6(n-1)`