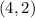The distance

between
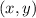
and
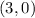
is:
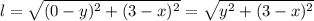
Since the equation of the hyperbola is
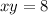
, we can get

by itself and end up with
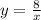
which we can plug into our distance formula:
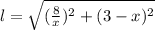
To make calculation easier, we'll square both sides:

and create a new variable

:
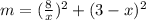

Differentiate both sides:

Minimum distance is achieved when
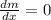
:
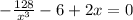
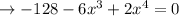
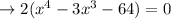

To find a value of

, you can use methods like synthetic division and get the answer

Plug into
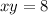
:
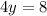
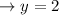
So the closest point on the hyperbola to
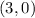
is