Answer:
The vertex is (3,-16) and axis of symmetry is 3
Explanation:
The vertex of a quadratic equation
 is calculated as
is calculated as
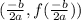
and the axis of symmetry is

Compare equation
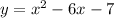 with
with

Where a= 1 and b = -6
so,
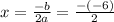
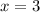
Now, put the value of x=3 in
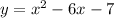



Therefore, the vertex is (3,-16) and axis of symmetry is 3