Exponential Decay Function
An exponential decaying function is expressed as:
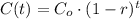
Where:
C(t) is the actual value of the function at time t
Co is the initial value of C at t=0
r is the decaying rate, expressed in decimal
The initial area of a forest is Co=3,900 squared km. The rate of decay is r=6.25%, expressed in decimal, r = 6.25/100 = 0.0625
Substituting in the formula:

Where t is expressed in years. Operating:
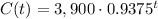
After t=5 years, the area of the forest is:
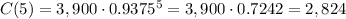
The above result was rounded to the nearest integer.
The area of the forest will be 2,824 square km after 5 years