Question

Select the outlier in the data set. 7 58 62 68 65 86 72 76 74 If the outlier were removed from the data set, would the mean increase or decrease?

Answer 1

7 is an outlier.

Data:

7, 58, 62, 68, 65, 86, 72, 76, 74

Let us rearrange the data

7, 58, 62, 65, 68, 72, 74, 76, 86

To know if a number is an outlier, it is usually either:

1. Lower Outlier Threshold = Less than Q1 + 1.5 x IQR

2. Higher Outlier Threshold = Greater than Q3 - 1.5 x IQR

where IQR is the interquartile range

Q1 is the First Quartile

Q3 is the Third Quartile.

Now we have to find Q1, Q3, and IQR.

The formulas are given below:

`\begin{gathered} Q1=((1*(n+1)))/(4)^(th) \\ \text{where n is the number of values in the dataset} \\ \\ Q3=((3*(n+1)))/(4)^(th) \\ \\ \text{IQR}=Q3-Q1 \end{gathered}`

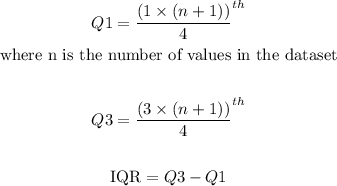
n = 9 (according to the question)

Thus, with these formulas, we can find the Q1, Q3, and IQR

`\begin{gathered} Q1=((1*(9+1))^(th))/(4) \\ Q1=(10)/(4)^(th)=2.5^(th) \\ Q1\approx3^(rd) \end{gathered}`

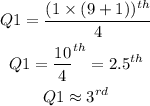
Therefore, the first Quartile Q1 is in the third position in the arranged data:

7, 58, 62, 65, 68, 72, 74, 76, 86

Q1 = 62.

Now we solve for Q3:

`\begin{gathered} Q3=((3*(9+1))^(th))/(4)=((3*10)^(th))/(4)=(30)/(4)^(th) \\ Q3=7.5^(th)\approx8^(th) \end{gathered}`

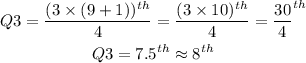
Therefore, the third Quartile Q3, is in the 8th position in the arranged data:

7, 58, 62, 65, 68, 72, 74, 76, 86

Q3 = 76

Now, we can calculate IQR as:

Q3 - Q1 = 76 - 62 = 14

Thus, IQR = 14

Now we can test which values are outliers.

`\begin{gathered} LowerOutlierthreshold=Q1-1.5* IQR \\ \text{Lower Outlier }threshold\text{ = 62- 1.5}*14=41 \end{gathered}`

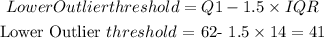
We have a value of 7 which is much lower than the Lower Outlier threshold value.

Thus 7 is an outlier.

Now let us check for the HIgher Outlier:

`\begin{gathered} \text{Higher Outlier threshold = Q3 + 1.5}* IQR \\ \text{Higher Outlier threshold= 76 + 1.5}*14 \\ \text{Higher Outlier threshold= 97} \end{gathered}`

We have no value from the dataset that is greater than 97, thus there is no upper outlier

Therefore, the final answer is = 7