Question

Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. xy = 9, x = 0, y = 9, y = 11

Answer 1

The volume of the solid obtained by rotating the region bounded by the curves about the x-axis is found using cylindrical shells, resulting in a total volume of 36π cubic units.

Step-by-step explanation:

To find the volume of the solid obtained by rotating the region bounded by the curves xy = 9, x = 0, y = 9, and y = 11 about the x-axis, we will utilize the method of cylindrical shells. The curves define a region in the xy-plane which, when rotated about the x-axis, forms a solid with varying radii. To apply the method, we first need to express the variable x in terms of y from xy = 9 to obtain x = 9/y.

Next, the volume of a representative cylindrical shell with thickness dy and height x = 9/y is given by the circumference of the shell (2πy) times the height (9/y) times the thickness (dy). This leads to the volume element dV = 2πy(9/y)dy = 18πdy. Integrating this volume element with respect to y between the limits 9 and 11 yields the total volume.

Using the integral calculus, the volume V is:
V = ∫911 18π dy = 18π [y]∫911 = 18π(11 - 9) = 36π cubic units.

Thus, the volume of the cylinder is 36π cubic units.

Answer 2

When integrating using shells, the first step is to plot the graph. I personally plotted it with the x and y axis switched, because it aids me in picturing the graph. The integral ranges from 9 to 11, since those are the limits from the two lines y = 9 and y = 11. The reason that these are the limits is because it is rotating around the x, not the y.

`\int\limits^(11)_(9)`
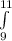
Now that you have the limits of the integral, you have to find what goes inside it.
Because you are integrating using shells, you need to remember to include the
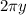
`2\pi y` Again, there is a y here instead of an x, because you are rotating around the x axis. Then you just need to input the function f(y). If you look at the graph that you (hopefully) plotted, you can see that this function ranges between the y axis and the curve
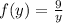
`f(y) = (9)/(y)`. Put together the pieces, and you have the integral

`\int\limits^(11)_(9) {2 \pi y*f(y)} \, dy`
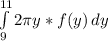
After substituting in
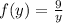
`f(y) = (9)/(y)`, you get

`\int\limits^(11)_(9) {2 \pi y*(9)/(y)} \, dy`
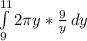
Simplified, this is
`18\pi\int\limits^(11)_(9) \, dy`
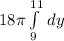
Integrating, we get
`18\pi * 2`

Therefore, the solution is
`36 \pi`

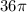
Note: I didn't spend very much time reviewing these integrals, so I may be incorrect.