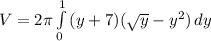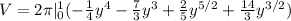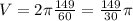Question

Use the method of cylindrical shells to find the volume V generated by rotating the region bounded by the given curves about y = -7. y=x^2, x=y^2.

Answer 1

Attached is a diagram setting up the problem.
Because the axis of rotation is horizontal and we are using shell method, the radius will be in the y-direction and integration will need to be in terms of "y".

The general formula for shell method is:

`2 \pi \int\limits^a_b {r(y) h(y)} \, dy`

r(y) is the radius as shown in diagram and is equal to the distance from y=-7 to upper curve x=y^2. This is distance from y=-7 to x-axis plus y-value along curve.
---> r(y) = y+7

h(y) is height of shell represented as x-distance between the 2 curves.
y =x^2 --> x = sqrt(y), x = y^2
----> h(y) = sqrt(y) - y^2

The limits are determined by y-values of intersection of 2 curves.
y^2 = sqrt(y) ---> y^3 -y = 0 -----> y = 0,1

Now we can write the integral:

`V = 2 \pi \int\limits^1_0 {(y+7)(√(y) -y^2)} \, dy`

`V =2 \pi \int\limits^1_0{(-y^3-7y^2+y^(3/2)+7y^(1/2))} \, dy`

`V = 2 \pi |^1_0 (-(1)/(4)y^4 -(7)/(3)y^3 +(2)/(5)y^(5/2)+(14)/(3)y^(3/2))`

`V = 2\pi (149)/(60) = (149)/(30) \pi`