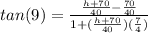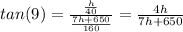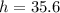Question

A flagpole is located at the edge of a sheer y = 70-ft cliff at the bank of a river of width x = 40 ft. See the figure below. An observer on the opposite side of the river measures an angle of 9° between her line of sight to the top of the flagpole and her line of sight to the top of the cliff. Find the height of the flagpole.

Answer 1

I would solve this using tangents. Let h be height of flagpole.
Set up 2 right triangles, each with a base of 40.
The larger triangle has height of "h+70"
Smaller triangle has height of 70.

Now write the tangent ratios:

`tan A = (h+70)/(40) , tan B = (70)/(40)`

Note: A-B = 9
To solve for h we need to use the "Difference Angle" formula for Tangent

`tan (A-B) = (tanA - tanB)/(1+tan A tan B)`
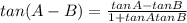
Plug in what we know:

`tan(9) = ( (h+70)/(40) - (70)/(40))/(1+ ((h+70)/(40))((7)/(4)))`

`tan (9) = ( (h)/(40))/( (7h +650)/(160)) = (4h)/(7h+650)`

`h = (650 tan(9))/(4-7 tan(9))`

`h = 35.6`