Question

Calculate the wavelength of a photon (in nm) that has the frequency of 5.66x10^14 Hz

Answer 1

The wavelength of the photon is 0.0053nm

Explanation:

Given data

Frequency of the photon = 5.66 x 10^-4 Hz

Let x represents the wavelength of the photon

To determine the wavelength of the photon, we need to apply the below formula

`\begin{gathered} C\text{ = f x }\lambda \\ \text{where} \\ c=\text{ sp}eed\text{ of light} \\ f\text{ = frequency} \\ \lambda\text{ = wavelength} \end{gathered}`

Recall that, the speed of light is 3 x 10^8 m/s

The next process is to substitute the values into the above formula

`\begin{gathered} c\text{ = f}\lambda \\ \text{Divide both sides by f} \\ (c)/(f)\text{ = }(f\lambda)/(f) \\ \lambda\text{ = }(c)/(f) \\ \end{gathered}`
`\begin{gathered} \lambda\text{ = }(3\cdot10^8)/(5.66\cdot10^(14)) \\ \lambda\text{ = }(3)/(5.66)\cdot10^{8\text{ - 14}}^{} \\ \lambda\text{ = 0.53 }\cdot10^(-6) \\ \lambda\text{ = 5.3 }\cdot10^(-7)m \\ \lambda\text{ =}0.0053nm \end{gathered}`

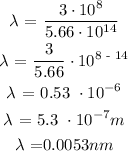
Therefore, the wavelength of the photon is 0.0053nm