Firstly, for us to solve this problem, we must remember that the distance between each maximum can be written as:
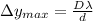
Where D is the distance from the slit to the screen, d is the distance between each slit and lambda is the wavelength. Thus, we can calculate this as:
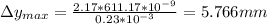
Thus, the distance from the central max (y0) and third max (y3) is three times this distance:
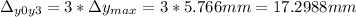
Then, our final answer is delta=1.73cm