Question

Monochromatic light passes through two narrow slits 0.23 mm apart and forms an interference pattern on a screen 2.17 m away. If light of wavelength 611.17 nm is used, what is the distance from the center of the central maximum to the center of the third order bright fringe in centimeters?

Answer 1

Firstly, for us to solve this problem, we must remember that the distance between each maximum can be written as:

`\Delta y_(max)=(D\lambda)/(d)`

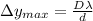
Where D is the distance from the slit to the screen, d is the distance between each slit and lambda is the wavelength. Thus, we can calculate this as:

`\Delta y_(max)=(2.17*611.17*10^(-9))/(0.23*10^(-3))=5.766mm`

Thus, the distance from the central max (y0) and third max (y3) is three times this distance:

`\Delta_(y0y3)=3*\Delta y_(max)=3*5.766mm=17.2988mm`

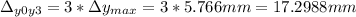
Then, our final answer is delta=1.73cm