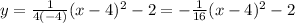Question

Give the equation of a parabola with a focus of (4, -6) and a directrix of y=2

Answer 1

Equation of Parabola is:

`y = (1)/(4p) (x-h)^2 + k`
where (h,k) is vertex and p = k - directrix
The vertex can be found by taking midpoint between focus and directrix:
Notice we will use y-coordinate since directrix is horizontal line (y=?)

`mid = ((-6) +2)/(2) = -2`
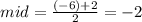
This is the y-value of vertex or k. The x-value of vertex is same as focus.

`(h,k) = (4,-2)`
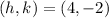
Next find p:

`p = k - d = -2 - 2 = -4`
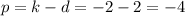
Finally we can write equation of parabola by plugging in values for h,k,p:

`y = (1)/(4(-4))(x-4)^2 -2 = - (1)/(16)(x-4)^2 -2`