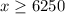Answer:
An inequality to find the amount of sales she must have to reach her goal is
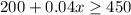 and
and
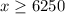
Explanation:
Let x be the amount of sale of this week .
Now we are given that commission equal to 4% of her sales.
So, commission =
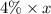
=

=
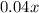
Since we are given that A salesperson earns $200 per week plus a commission equal to 4% of her sales.
So, He earns in this week =
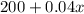
Now we are given that This week her goal is to earn no less than $450.
So, equation becomes:
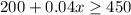
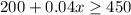
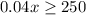

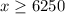
So, the total amount of sale must be greater than or equal to 6250
Hence an inequality to find the amount of sales she must have to reach her goal is
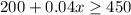 and
and